To clearly show the features and effectiveness of cross validation, it is worth taking a look at how it appeared. That is, to recall the previous approaches.
Why do we even divide the dataset into a training and a test one?
The model needs to be evaluated in order to understand how well it works, if we train the model on all the data, then we will not know how well it makes predictions. Even if we then do tests on the same data on which the model was trained, it will give an excellent result, but in fact we already know the target values in the available data, the main task is to predict the values of the target variable on the new data.
This implies the first rule - the model must be tested on data that it does not know. This will guarantee a test of her real abilities.
There are observations or objects that affect each other in time, as the weather today affects the weather tomorrow, and there are objects whose order is independent - such as, for example, car sales ads in Avito.
Let's consider the case when each sample object is independent of each other in time.
TRAIN/TEST
One training subsample and one test sample is the simplest and most frequently used solution. The data is divided into two parts with the selected ratio, typical of
which are 2/1 or 4/1

Now the model is tested on real data and you can get a more reliable result.
Why is it more reliable and not reliable?
Let's analyze a visual situation when our sample consists of 12 red apples and 4 green ones. Model learn to separate apples red from green.

There may be a situation when there will be only red apples in the training sample, and only green apples in the test sample.
In this case, the model did not have time to get acquainted with the distinctive features of green apples and it turns out on the test that the model did not learn anything.
That is why the data needs to be mixed so there is much more chance that the target features will be evenly distributed and the training and test samples will together reflect the sample from which they were obtained.

That's how the problem was solved uneven distribution in the data.
But there is always the possibility of incorrect partitioning of the sample, even with mixing...
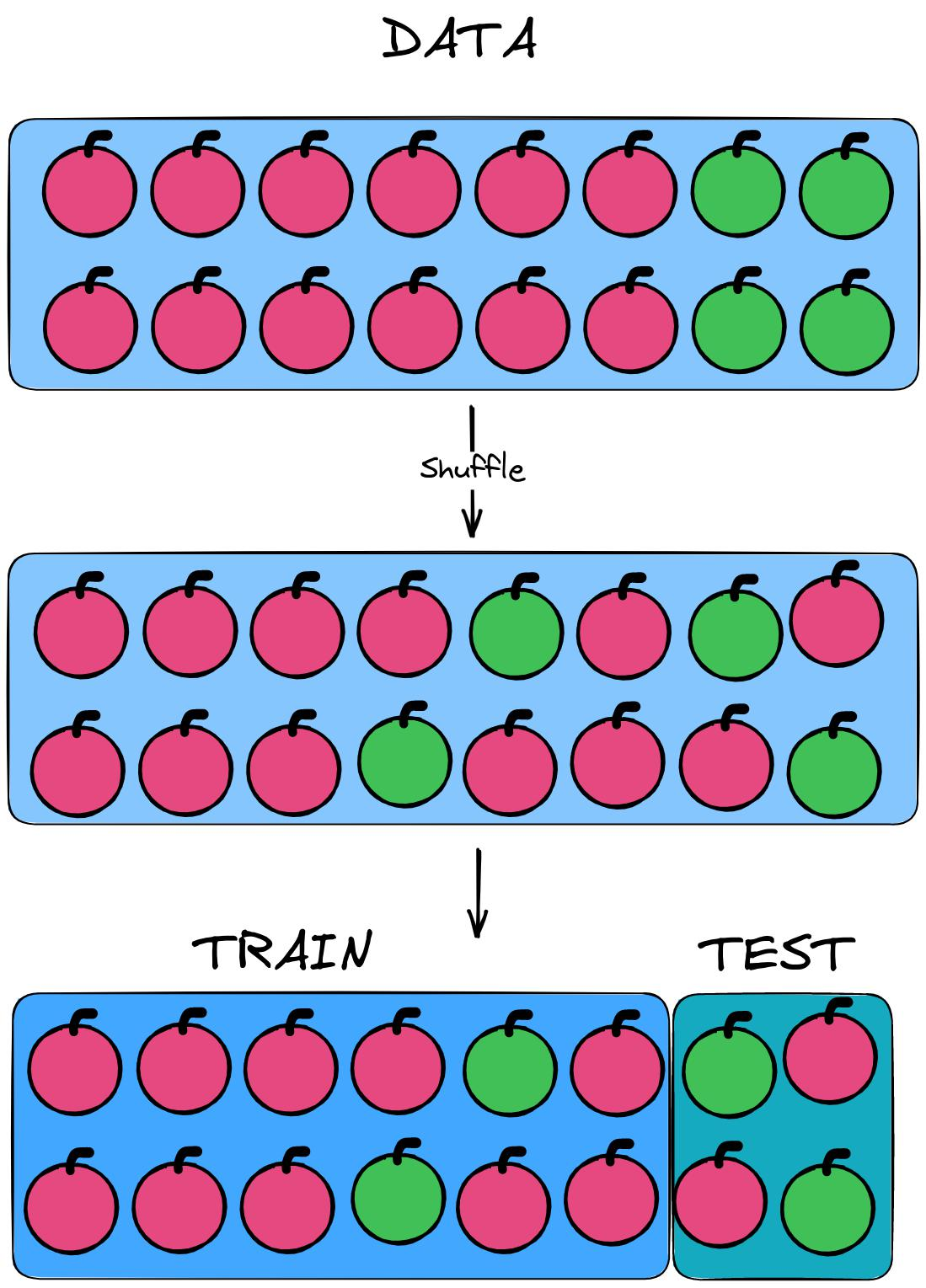
How do we accurately and correctly distribute the class of green and red apples?
It is necessary to count the number of green and red apples, and then in each class to make a division into a training and test part. In this case, you will get two train tests - (9/3) red apples and (3/1) green ones.
So, in order to solve the problem of equalizing classes, you just need to count them and make a mini-train test subsample for each class, and then simply combine the trains and tests into a final validation sample.

However, even if the data were perfectly distributed across the samples, in fact the model predicted only 4 specific apples out of 16. That is, she did not try to classify the other 12 options, so much so that she did not study on them. Behind this lies the unknown. We cannot say for sure that the model coped with all the data, because we checked only one combination.
The option of using more data is sequential mixing of the sample and training, but you can't be 100% sure that at a certain iteration we have exactly tried all the options, so the method is also overhead.
The evolution of this idea is cross-validation - when sequential training and tests are done on the same order and data set. Yes, in this way, the resulting models in their totality were trained on all data and tested on all data, too.
The full name of the approach is k-fold cross-validation. It implies that the dataset is divided into k pieces, one of which is a test, and the rest are training..
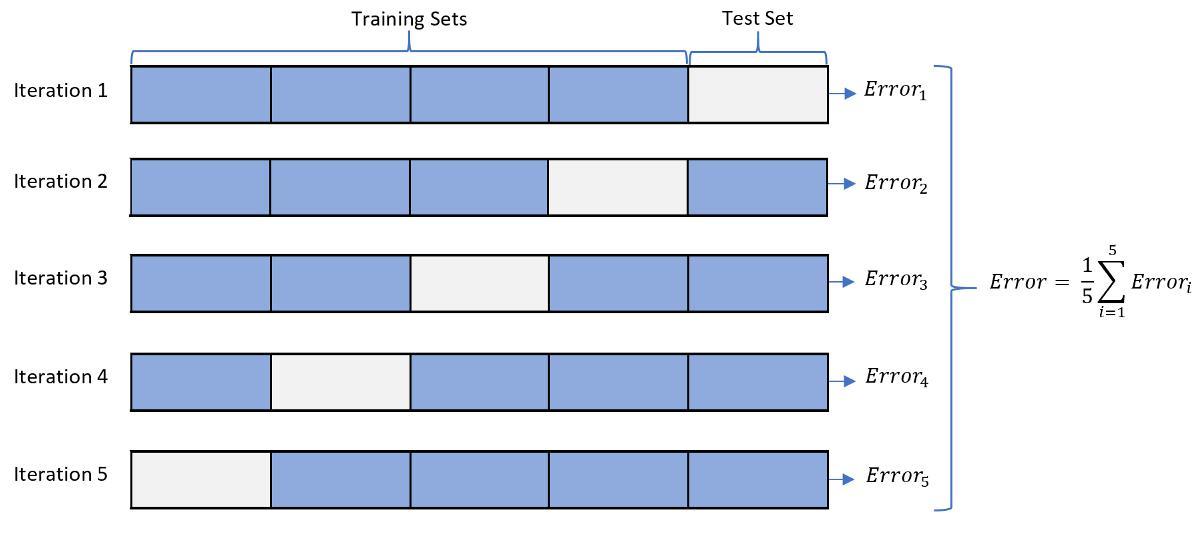
Next, the test fold is sequentially swapped with the training tails in such a way that all possible locations of the test chunk are sorted out. There are k combinations in total.
In the picture above, k=5. Trained and tested 5 identical models, and then there is
the average of their results. All data has been used, and the average result is the most accurate estimate of the model selected for this data.
If we combine this approach with the equalization of the train-test ratio for each class, we get a stratified cross-validation
If our target feature is three unevenly distributed classes, then by applying k-fold cross validation, you can see how classes in trains and tests will vary seriously, somewhere there will not be one of the classes at all - therefore, models trained on such data will be bad.

Stratified cross-validation will divide the samples by preserving the percentage of objects for each class.
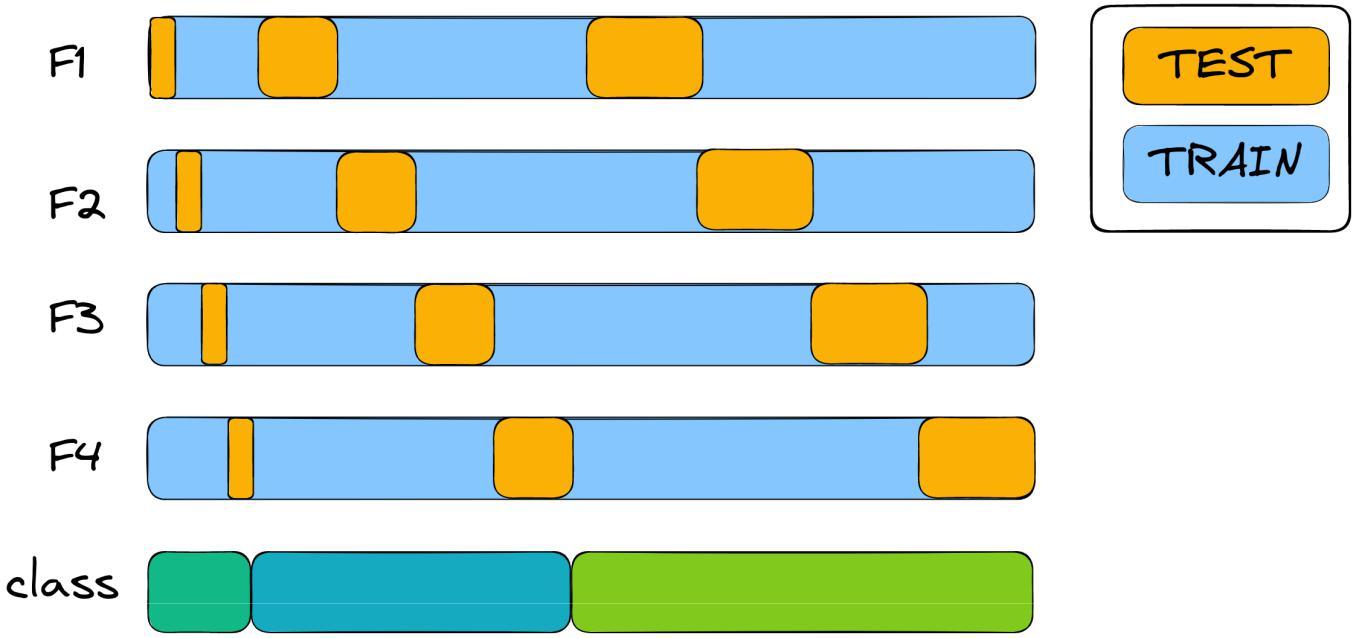
Thus, stratified cross-validation combines several approaches and is the most effective method of splitting the dataset for validation.
In the next article, I will continue to reveal the topic of validation and explain the features of its application on time series.
Author: Andrey Epifanovsky
